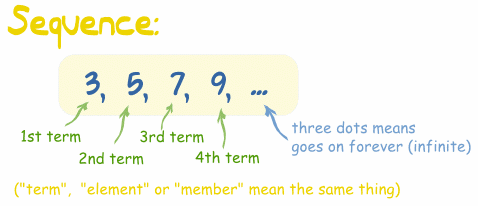Linear Programming

Vertices:	0,6		0,0		6.0
Constraints	Objective Function: 3x+4y
x ≥ 0 y ≥ 0 x + y ≤ 5	3(0)+4(6)=24	3(0)+4(0)=0		3(6)+4(0)=18

Vertices:	-5,4		0,6		0,4
Constraints	Objective Function: 2x+5y
x ≥ 0 y ≥ 0 x + y ≤ 5	2(-5)+5(4)=10	2(0)+5(6)=30		2(0)=5(4)=20

Vertices:
Constraints	Objective Function:
x ≥ 0 y ≥ 0 x + y ≤ 5

Vertices:
Constraints	Objective Function:
x ≥ 0 y ≥ 0 x + y ≤ 5

Vertices:
Constraints	Objective Function:
x ≥ 0 y ≥ 0 x + y ≤ 5

Vertices:
Constraints	Objective Function:
x ≥ 0 y ≥ 0 x + y ≤ 5

graphing exponential equations.

compound interest formula

Statistics

Statistics Data

ccalgebra-ronaldayers

General Forms Of A Sequence: 

What is a sequence, And how do u know which sequence it is???

A sequence is an ordered list of numbers or objects. There must be a pattern in the way these numbers or objects are organised. We usually refer to this pattern as a common difference or ratio. In this revision I will be concentrating particularly on the two types of sequences. That is the Arithmetic and geometric sequence.

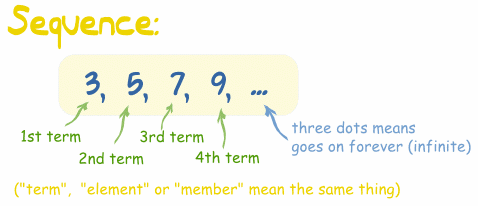The types of sequences

Arithmetic progression/sequences

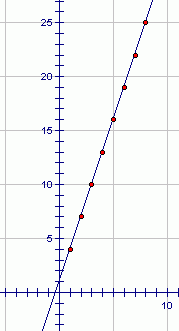
An arithmetic progression or arithmetic sequence is simply a sequence of numbers with a common difference and this common difference has to be constant. For example: 2, 4, 6, 8, 10 is an arithmetic progression sequence with common difference 2.So you have the arithmetic sequence 2, 4, 6, 8, 10, 12; In general we write the formula for this sequence as:a_k+1 = a_k+2Where k is the position of a term such as the previous term. This type of sequence where the first term of the sequence and the formula is called an iterative or inductive sequence. It uses an inductive or iterative formulae, this is true for all types of formulas including the geometric sequences. The first term of the sequences and the formula is required. The first term is called a₁, the second term a₂, third term a₃ and so forth…
a₁ = 2You can go further to generate the following terms in the sequence;a₂ = a₁+2a₃ = a₂+2a₄ = a₃+2a₅ = a₄+2On the other hand you might have a sequence with a deductive or direct formulae; For example for our sequence above the formula would be:
a_k = 2k+0where k is the position of the term in question. I have add the +0 to signify the process which must be carried out where we subtract the difference from the first term while forming the formula. The same formula will generate the above sequence except we do not need the first few terms of the sequence to find the following sequences.

Geometric progression/sequences

A Geometric sequence is a sequence of numbers where each term in the sequence is found by multiplying the previous term with a with a unchanging number called the common ratio. For instance, the sequence 2, 6, 18, 54, … is a geometric sequence with common ratio 3. Similarly with 10, 5, 2.5, 1.25, … which is a geometric sequence with common ratio 1/2.

In the first instance the sequence 2, 6, 18, 54, ….

a₁ = 2
a₂ = a₁ x 2
a₃ = a₂ x 2
a₄ = a₃ x 2

In general we write the formula for the above geometric sequence as:
a_k+1 = a_kx3

Domain: The X Values
Range: The Y ValuesEnd Behavior: Describes the two ends of an equation.

Absolute Max/Min: 1 point that is highest/lowest on a graph.

Local Max/Min: More than 1 point that is highest/ lowest on a graph.

Interval of Increase: Section of a graph where the Y values are increasing/ describes them in terms of the X values.

Interval of Decrease: Section of a graph where the X values are increasing/  describes them in terms of the Y values.

X intercepts: The point where the graph crosses the X-axis.

Y intercepts: The point where the graph crosses the Y-axis.

Symmetry: Based on whether the graph is even or odd or even neither.

Even/Odd/Neither: Even is ABOVE the origin/Odd is ON the origin/ and Neither is BELOW the origin OR NOT on the origin.

Asymptotes: The line that gets closer but never touches.Function: Passes the vertical line test 

only.

one to one: passes both the vertical and horizontal line test.

Increasing AND Decreasing Funtions

Both Increasing and Decreasing On One Graph

One to One Graphs 

Even & Odd Functions

Asymptotes

X and Y intercepts